Cursul 2: Diamantele Iluminării
Primul nivel al perfecțiunii înțelepciunii
(Prajna Paramita)
Inspirate după învățăturile lui Geshe Michael,
traducere a conferințelor Lamei Dvora Tzvieli
Lecția 9
Aici poți descărca versiunea PDF a acestei lecții .
Revenim la demonstrația celor trei cunoașteri.
1. În primul rând trebuie să existe un subiect. Exemplu: „Să considerăm soarele”. Deci tema mea este soarele.
2. Ce vreau să demonstrez? Că „soarele nu este albastru”.
3. Argumentul este „Pentru că este galben.”
Patru este opțional. Pentru ca demonstrația să fie bună trebuie să existe anumite legături între 1, 2 și 3.
a. Argumentul trebuie să fie legat de subiect
Deci prima legătură care trebuie să existe, este că argumentul pe care îl dau în 3, trebuie să fie legat de subiect. Ne referim la relația între 3 și 1, sau între cauză și subiect.
Pentru că dacă subiectul meu este soarele și dăm argumentul: „că luna este roșie”, înseamnă că 1 și 3 nu sunt legate.
În budism, argumentul poate fi orice. Faptul că nu este bun – asta este altă chestiune. Deci, trebuie să existe o legătură între argumentul pe care îl dăm și subiect.
O demonstrație bună trebuie să înceapă de la un numitor comun între adversari
Cei doi adversari trebuie să fie de acord cu atributul subiectului. Amândoi trebuie să fie de acord că „a fi galben” este un atribut al soarelui. Pentru că dacă spun: „Soarele este galben”, iar adversarul meu spune: „Ce legătură are galbenul cu soarele?”, nu pot merge mai departe cu el, nu-i așa?
O astfel de demonstrație în budism nu este bună. Chiar dacă am dreptate sau chiar dacă și alții vor fi de acord cu mine ca soarele este galben, în cazul în care adversarul meu nu este de acord cu mine că soarele este galben, nu pot continua demonstrația. Trebuie să merg înapoi. Ce înseamnă asta? – Voi spune, „soarele are culoare”. Dacă nici cu asta adversarul nu este de acord, trebuie să merg din nou înapoi. „Are niște proprietăți”. Deci trebuie să merg înapoi, până când găsesc un numitor comun cu adversarul meu.
În demonstrația budistă, dacă nu am început cu un numitor comun asupra căruia suntem amândoi de acord, nu este bine. Deci, în acest sens, demonstrația budistă este diferită de cea în matematică sau în logica occidentală.
În exemplul nostru, adversarul este de acord cu noi că „soarele este galben” și trebuie să fie de acord că „nimic nu poate fi și galben și albastru în același timp”. Adică – are deja toate elementele demonstrației, pur și simplu nu a trecut prin logica care le-a legat între ele, așa că nu i-a trecut prin minte că „soarele nu poate fi albastru”. Îl ajutăm să lege capetele.
Amândoi suntem de acord că „soarele este galben” și amândoi suntem de acord că „nimic nu poate fi galben și albastru în același timp.” Și acum – doar îl conducem prin logică pentru a-l face să înțeleagă că „soarele nu poate fi albastru”
Deci, adversarul trebuie să fie de acord cu mine în ceva, iar dacă știu să dezbat bine, îl voi duce pas cu pas până când el va spune: „Dö – corect ”, iar atunci demonstrația s-a încheiat.
b. Trebuie să existe o legătură logică între argument și afirmație
În al doilea rând, legătura dintre argument și afirmație trebuie să fie corectă.
-
- Subiectul: „Soarele”
- Afirmația: „El nu este albastru.”
- Argumentul: „Pentru că este galben.”
Dacă argumentul (3) este adevărat, atunci afirmația (2) trebuie să fie întotdeauna adevărată.
În cazul nostru: „Pentru că soarele este galben, atunci nu este albastru”. Sau din 3 să rezulte 2. (3 ⇒ 2)
c. Trebuie să existe o relație inversă între afirmație și argument
Putem merge și invers. Dacă afirmația nu este adevărată, argumentul trebuie să fie de asemenea fals. Dacă ‹ nu 2 ›, atunci trebuie să fie ‹ nu 3 ›.
~ 2 ⇒ ~ 3
Exemplul 1: Putem spune: „Dacă soarele este albastru, atunci nu ar putea fi galben”.
Exemplul 2: „Dacă este fum, trebuie să fie foc”.
Un alt mod de a spune același lucru este: „Dacă nu este foc, nu este fum.” sau „Nu există fum fără foc.”
Atenție: aceasta nu este o chestiune de echivalență! (dacă și numai dacă)
Aici nu vorbim despre „dacă și numai dacă” ca în matematică. Adică „dacă a atunci b și dacă b atunci a” , sau ambele propoziții sunt adevărate sau ambele false.
Dacă a ⇒b, atunci non a ⇒ non b ( ~ a ⇒ ~ b)
Dacă din a rezultă b, atunci, dacă eu nu am b nu poate exista a. Pentru că întotdeauna când există a, există b. Caut, există un b? Nu, nu există b, deci nu poate exista nici a. Deci este practic același lucru, cu alte cuvinte.
Un alt exemplu: „Dacă este ploaie, trebuie să fie nori.” ; „Dacă nu sunt nori, nu poate fi ploaie”.
Prin urmare, pentru a verifica dacă demonstrația este bună, este suficient să verificăm că primele două relații au loc, pentru că a treia are loc automat.
Cele trei tipuri de cunoașteri nu există ca unul
Să intrăm în demonstrația celor trei cunoașteri.
A. Există ele ca unul?
Nu, pentru că sunt trei. Sunt trei -> am terminat. Nu există ca unul.
Iată formularea tibetană a acestei părți a demonstrației:
 shi lam nam sum chuchen
shi lam nam sum chuchen
 dendrup kyi chiktu madrup te
dendrup kyi chiktu madrup te
 chache yin pay chir
chache yin pay chir
1. Shi lam nam sum chuchen
Shi = baza,
Lam = cale,
Nam = atotcunoașterea,
Sum = trei,
Chuchen = să considerăm.
Să considerăm cele trei tipuri de cunoașteri.
2. Dendrup kyi chiktu madrup te
Dendrup = existență reală,
Kyi = prepoziție,
Chiktu = ca unul
Madrup = nu există.
Ele nu există cu adevărat ca unul.
3. Cha che yinpay chir
Cha che = are părți,
Yinpay chir = deoarece.
Deoarece au părți.
Să considerăm cele trei tipuri de cunoașteri.
Ele nu există cu adevărat ca unul
Deoarece ele au părți.
Cele trei relații trebuie să fie adevărate:
a) 3 este legat de 1. ( argumentul este legat de subiect)
b) Dacă 3 este adevărat, atunci 2 este adevărat, ( dacă au părți atunci nu există ca unul)
c) Dacă 2 este negat, atunci 3 este negat. ( dacă există ca unul, rezultă că nu au părți)
B. Există cele trei tipuri de cunoașteri ca mai multe?
Aceasta este o demonstrație separată și diferită de cea anterioară și mult mai relevantă pentru înțelegerea vacuității. Dacă ceva există ca multe, atunci are părți. Deci fiecare dintre părți trebuie să existe și vom încerca să infirmăm acest lucru.
Dar înainte de a ajunge la miezul demonstrației, să o ilustrăm în cazul pixului care este mai simplu.
Exemplul 1 – Pixul
A. Pixul nu există ca unul ( indivizibil)
Oare pixul există ca unul? Nu! De ce? Pentru că are părți. Are o parte neagră și una albă, sau are o parte stângă și o parte dreaptă. Deci pixul are părți.
Mai multe moduri de a privi asupra acestui aspect.
– Pot să văd pixul fără să-i văd părțile?
Când mă uit la acest pix, trebuie să văd partea neagră și partea albă. Pentru a vedea un pix, trebuie să mă uit la părțile lui, nu-i așa? Dar când mă uit la părțile lui, ce văd? Părțile lui! Nu văd un pix. Aceasta este baza acestei dovezi. Nu mai este un lucru care nu poate fi divizat/fragmentat. Asta e toată ideea. Vreau să caut unde este pixul. Eu zic: “Hai să văd, există un singur lucru aici și este pix? – Nu, nu este un singur lucru, ci două, aici este negru și aici este alb.” Deci, pentru a putea vorbi despre un pix, trebuie să-i văd părțile. Dar când mă uit la părțile lui, văd părți, și nu văd un pix.
Vedem diferite părți și indicii, apoi desenăm în mintea noastră o imagine completă a unui pix pentru lucrul care este acolo și credem că acolo este un „pix”, mai degrabă decât o construcție mentală. Dacă percepem părțile, nu putem percepe întregul (unul). Dacă nu am fi perceput părțile lui, nu am putea vedea deloc obiectul ca existent.
– Ce deține calitatea de pix?
Se poate spune altfel. Există vreun lucru care să dețină calitatea de a fi un pix?
Să vedem: negrul deține calitatea de pix? Nu, nu, negru este culoarea neagră a pixului, nu este pixul. Să vedem, albul deține calitatea de pix? Nu, este partea albă, nu este pix.
Caut unde este pixul? Văd aici că sunt multe lucruri, și nu găsesc în niciunul conceptul de „pix”. Nu există un singur lucru care să țină acest concept de pix.
Putem spune mai simplu, dar puțin mai abstract. Pentru a demonstra că ceva nu este unul (întreg indivizibil), mă duc și găsesc părți în el. Deci, nu este un singur lucru, pentru că este alcătuit din părți. Deci, orice lucru care are părți, nu este unul (o unitate).
Ce lucru nu are părți? Nu există așa ceva – totul are părți.
Aceasta este o chestiune semantică, deoarece decidem că această colecție va fi un singur lucru, numit pix.
Aceasta este toată ideea, căutăm „existența lui adevărată” – și nu o găsim. Avem în minte ideea de pix, dar nu este pixul care există „cu adevărat”. Vreau să văd dacă el „cu adevărat” există.
Este oare vreun pix aici despre care oricine ar spune: „Ah, pix!”? Vrem să demonstrăm că nu există așa ceva. Dacă el ar exista într-adevăr ca pix în sine, atunci oricine va veni l-ar vedea ca pix. Așa că spun: „Hai să ne uităm, unde este acest pix?” Apoi spun: „El are părți, așa că dacă el există, el nu există ca unul/ca unitate, nu-i așa?
B. Pixul nu există ca multe
Dacă pixul există ca multe, atunci să ne uităm la părțile lui.
Deci părțile sale trebuie să existe cumva. Hai să vedem. Această parte, există ca unul sau mai multe? Și el are părți, nu-i așa? Nu există nimic care să nu aibă părți. Deci demonstrația s-a terminat.
-
- El nu există ca unul – pentru că are părți.
- Nu există ca multe – de ce?
– De ce nu există pixul ca multe?
Dacă el este multe, atunci ar trebui să fie format din părți, dintre care fiecare există.
Când spun „multe”, ne referim la mult, numeros. Deci are componente, sunt multe componente. Atunci fiecare dintre componente ar trebui să existe pentru ca eu să am multe; Trebuie să am o colecție de părți, să am o „colecție”.
– Fiecare parte are propriile sale părți
Să ne uităm la părți. Să luăm această parte. El trebuie să fie acolo astfel încât să am o colecție de părți. Hai să vedem, această parte există? El există ca unul sau ca multe? El nu există ca unul pentru că are părți. Are o proeminență aici, și are o proeminență aici, deci are părți, și deci nu există ca unul.
Să continuăm să căutăm. Această parte a lui, este una sau mai multe? El este multe pentru că are partea dreaptă și are partea stângă.
Nu putem ajunge niciodată la acele unități care alcătuiesc cele multe.
„Multe” înseamnă că „are părți”. Unde sunt părțile? Nu găsim părțile.
Pentru ca pixul să existe ca mai multe, trebuie să am unități care îl compun, și care există, și apoi colecția există. Dacă unitățile există, atunci și colecția există.
Așa că mă duc să caut unitățile, și nu le găsesc, pentru că fiecăreia dintre ele, i se aplică aceeași logică.
Nu pot să găsesc nicio unitate în acest pix. Nu găsesc nimic în acest pix care să existe ca unitate, ca ceva indivizibil. Deci, cum va fi acolo un pix? Nu găsesc nimic despre care să spun: „Aceasta este o unitate, iar lângă ea este o altă unitate”.
– Chiar și atomii pixului au propriile lor părți.
De ce? Pentru că atomii au o parte stângă și una dreaptă. Atomul are nucleu si electroni. Nucleul atomului are protoni și neutroni, și așa mai departe. Și ele la rândul lor au părți
– Dacă nu putem găsi părțile – nu putem găsi întregul
Vrem să vedem dacă acest lucru există ca o colecție de părți. Pentru asta am nevoie de părți. Căutăm părțile – dar nu le găsim, pentru că și ele au părți, iar aceste părți au la rândul lor alte părți. Și acest proces nu are un sfârșit.
Deci, dacă nu am părți, pentru că părțile nu au părți și încerc să mă întorc la întreg, cum va fi el întreg dacă nu are părți? Cum poate să fie o colecție, dacă nu are părți? O colecție de ce?
Aceasta este demonstrația.
Toată ideea de aici, merge spre gândirea noastră despre atomi.
„Multe” înseamnă că: „sunt unități discrete care alcătuiesc” – dar așa ceva nu există. Nu le putem găsi.
Întreaga noastră idee despre atomi este nefondată. Toată această idee presupune că există particule de bază, dar pe care nu le putem găsi.
Este foarte frustrant, și de aceea ne împotrivim, dar exact așa găsim vacuitatea. Așa vom găsi vacuitatea, prin faptul că, căutăm și suntem gata să fim în acest loc în care nu găsim nimic.
Deci, dacă pixul nu există ca unul (ca unitate), și nu există ca multe, atunci el nu există cu adevărat, pentru că nu mai este și un alt mod în care să poată exista.
Exemplul 2: Unde este Bucureștiul?
Să considerăm Bucureștiul. Unde este? Putem să-l arătăm pe o hartă. Dar harta nu este Bucureștiul, este doar o reprezentare a Bucureștiului.
Vedem parcuri, case, lacuri, dar unde este Bucureștiul în asta?
Noi nu dorim conceptul nostru de București, ci dorim Bucureștiul care „există cu adevărat”. Vrem să dovedim că nu există nici un București care să existe cu adevărat.
Pentru că unde este Bucureștiul? Dacă arătăm cu degetul spre lacul Herăstrău, el nu este București, dacă arătăm spre Piața Universității, nu este București.
Putem spune: Ah, dar toate împreună sunt București. Unde sunt împreună? Sunt în mintea noastră! Acesta nu este București, ci doar ideea noastră despre București.
Aceasta este problema noastră.
Avem conceptul de pix în cap, pe care îl proiectăm pe o colecție de date brute și credem că este un pix. Vorbim cu un concept care stă în capul nostru și suntem gata să plecăm la război pentru el. Suntem gata să intrăm în război pentru ceva ce nu există cu adevărat.
Oare întregul este însumarea părților sale?
Oare „Gabriela” este o colecție de părți?
Dacă tai o mână, mai este „Gabriela”? Cei mai mulți vor spune „da”. Și dacă aș tăia o altă mână? Și dacă tăiem capul? Nu mai știm. Cum ar fi să vedem în desenele animate că trupul merge fără cap.
Aceasta este exact ideea: este întregul o colecție a părților sale? Este „Gabriela” o colecție de părți? Dacă asta ar fi fost adevărat, atunci dacă ar veni un gândac și ar vedea această colecție de părți, ar spune: „Uite Gabriela”.
Dacă „Gabriela” ar fi o colecție de părți, atunci fără o mână nu mai sunt eu.
Ce anume nu este în ordine aici? De ce altceva mai avem nevoie pentru a avea o „Gabriela” aici? Este oare suficient să existe o anumită colecție de părți pentru ca aici să fie o „Gabriela”? Ce va spune Svatantrika?
Ea va spune că este nevoie de cineva care să denumească acest lucru „Gabriela”, fără asta ea este doar o colecție de părți.
Este nevoie să ne reamintim că scopul nostru în această lecție este să folosim argumentul „unul sau mai multe” pentru a arăta vacuitatea tuturor fenomenelor, că ele nu există cu adevărat.
Ultima discuție, care este de fapt foarte utilă, a alunecat spre o altă întrebare, și anume: „Cum există cu toate acestea, fenomenele”?, care este desigur cealaltă fațetă a monedei și, prin urmare, este legată de întrebarea vacuității, dar nu identică cu ea.
Numeroase demonstrații ale vacuității
Datorită faptului că oamenii au diferite stări sufletești, unele demonstrații vor fi acceptate de unii, altele de alții.
De aceea, marii Lama ne oferă o mulțime de demonstrații astfel încât omul să se lămurească în cele din urmă. Să ajungă să se convingă că lucrul în care crede că există cu adevărat și pentru care este dispus să-și sacrifice viața pentru el – nu a existat și nu va exista vreodată.
Și asta ne va schimba viața.
Ceea ce este corect față de pix, este corect și față de toate lucrurile.
Ceea ce dorim să facem, este de a lua demonstrația „unul sau mai multe”, pe care nu am terminat-o, pentru că am făcut-o doar pe pix – și să o aplicăm fiecărui lucru din lumea noastră. Și ce va fi atunci? Fiecare lucru va fi gol.
Dacă spun: „Fiecare lucru este gol”, atunci va trebui să iau fiecare lucru care există în lume și să arăt că este gol. Deci cum facem asta?
Clasificarea tuturor fenomenelor
Prima clasificare a tuturor fenomenelor: lucrurile care se schimbă și cel care nu se schimbă.
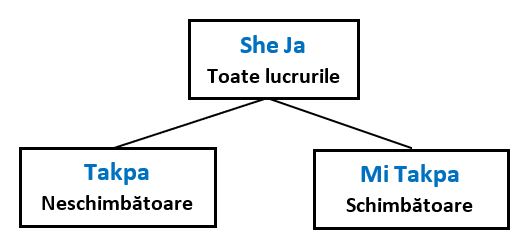
Orice lucru la care ne gândim, este fie schimbător/variabil, fie neschimbător/invariabil. Altă opțiune nu mai există.
Vom continua să descompunem lucrurile. Le vom lua mai întâi pe cele care se schimbă, apoi vom trece la cele care nu se schimbă.
Să luăm toate lucrurile care se schimbă.
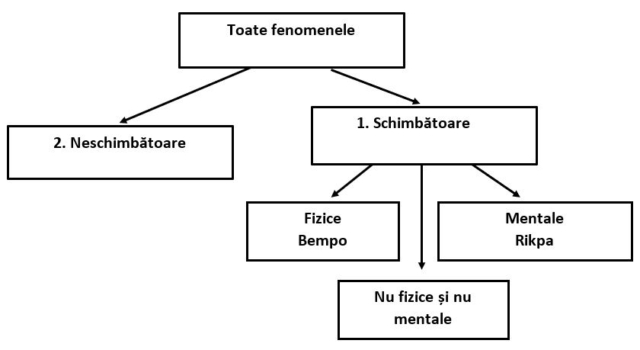
Lucrurile schimbătoare pot fi fizice sau mentale. Ele nu pot fi și una și alta.
Există lucruri care nu sunt nici una și nici alta? Da, sunt semințele karmice – bakchak.
Dacă ele ar fi mentale, ele ar trebui să fie un factor mental din lista factorilor mentali. Dar ele nu sunt. Nu există ceva care să fie și fizic și mental, dar există unele care nu sunt nici una, și nici alta, care sunt potențial. Ca amprentele karmice. Ele nu sunt încă lucruri mentale, pentru că încă nu s-au maturizat. Și cu siguranță nu sunt lucruri fizice, pentru că nu le putem atinge sau să le vedem la microscop.
Să mergem mai departe, să luăm lucrurile fizice.
Lucrurile fizice pot fi împărțite în lucruri fizice grosiere și subtile.
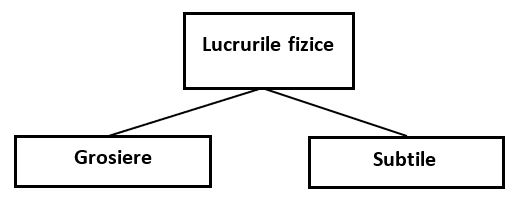
Ce înseamnă grosier și subtil?
- grosier, este lucrul fizic pe care îl vedem cu ochiul liber.
- subtil, este lucrul pe care îl putem vedea cu ajutorul dispozitivelor, adică particulele.
Fiecare lucru din lume are părți
Revenim acum la demonstrația că nu există nimic care să existe cu adevărat. În prima și principala etapă a demonstrației, vom trece în revistă toate cazurile posibile, și vom vedea că nu există nimic în lume care să nu aibă părți.
A. Lucrurile fizice grosiere au părți
Să considerăm lucrurile fizice grosiere, cum ar fi mâna mea.
Există ea oare ca unul? Nu, pentru că am degete și dacă acopăr câteva dintre degete, văd că mai rămâne o parte. Așa am demonstrat că are părți. Deci, mâna nu există ca unul.
Mâna are părți, și fiecare parte are alte părți, și așa mai departe. Degetul are articulații, articulațiile au celule, celulele au molecule, moleculele au atomi. Am terminat demonstrația.
Deci, am arătat că lucrurile fizice grosiere, nu există, nici ca unul, nici ca multe. Deci, cu lucrurile fizice grosiere, am terminat.
B. Chiar și lucrurile fizice subtile, cum ar fi atomii, au părți
Să vorbim despre atomi. Atomii au particule mai mici.
(În fizica particulelor, o particulă elementară este o particulă din care sunt compuse alte particule mai mari. De exemplu, atomii sunt formați din particule mai mici cunoscute sub numele de electroni, protoni, şi neutroni. Protonii și neutronii, la rândul lor, sunt compuși din particule mai elementare cunoscute sub numele de quarci. Una dintre problemele nerezolvate ale fizicii particulelor este de a găsi cele mai elementare particule – sau așa-numitele particule fundamentale – care alcătuiesc toate celelalte particule care se găsesc în natură și nu sunt ele însele alcătuită din particule mai mici.)
Nimeni nu va spune că există o particulă fundamentală, nici măcar în știință.
În Abhidharma Kosha nu se vorbește despre electroni și protoni, ci se spune că : „Sunt particule mici pe care nu le putem vedea” și aici se referă la atomi. Deci au o parte stângă și una dreaptă?
Trebuie să existe o parte stângă și una dreaptă. De ce? Dacă nu există partea stângă și partea dreaptă, atunci totul ar fi fost împreună, atunci nu era nicio parte grosieră – totul ar fi fost ca un punct geometric adimensional. (Euclid definește punctul ca fiind un obiect fără părți).
(Răspunsul la întrebarea 4 din teme: Atomii sunt un bun exemplu pentru a demonstra că lucrurile fizice subtile au părți. Dacă atomii nu ar avea părți, atunci când doi atomi s-ar fi atins unul de celălalt, ar fi trebuit să se atingă pe toată suprafața lor. Ei nu s-ar fi putut distinge deloc, și totul ar fi fost un mare atom. Ceea ce se întâmplă cu adevărat este, că un punct dintr-un atom atinge un punct al celuilalt atom. Acest lucru face ca celelalte puncte să fie mai apropiate sau mai îndepărtate unul de celălalt, și acest lucru demonstrează că atomul are părți, cum ar fi partea superioară, partea inferioară, partea din stânga sau din dreapta și așa mai departe.)
C. Lucrurile mentale au și ele părți
Ce sunt lucrurile mentale? De exemplu, ar putea fi mintea mea, ar putea fi funcții mentale: ca emoțiile. Pot fi afecțiunile mentale – acestea sunt lucruri mentale.
Au lucrurile mentale părți? Are mintea mea părți? Da, mintea are sentimente, are gânduri, are idei, deci are părți, nu-i așa? Mai mult de atât, pe linia temporală, există mintea din acest moment, apoi există mintea din momentul următor. Deci are părți pe linia temporală. Deci, indiferent de cum privim mintea, ea are părți.
Dar funcțiile mentale? Funcțiile mentale au părți? Sigur că au. Există sentimentul de iubire, există sentimentul de ură, există sentimentul de invidie, există părți. Nu este un singur lucru. Odată ce există părți și părțile au părți – am terminat. Există părți.
Deci lucrurile fizice au părți; Cele grosiere au; Cele subtile au; Cele mentale au; Am terminat cu toate lucrurile schimbătoare.
Contradicția la care se ajunge demonstrează greșeala – și anume ipoteza de bază că lucrurile există cu adevărat.
Scopul nostru aici este să arătăm că ipotezele de bază care presupun că lucrurile au existență de sine, duc la contradicții, și în acest fel ne consolidăm înțelegerea noastră despre vacuitate.
Știți care este diferența dintre un matematician și un fizician? Nu? – Fizicianului i se spune să facă ceai – are un ibric aici și are ceașca aici, așa că fierbe apa în ibric și toarnă apa în ceașca în care este un plic de ceai și iese ceai.
Matematicianului i se spune: Acum fă ceai – el se duce și pune apă în ibric. „Restul l-am făcut deja”.
Asta facem noi aici.
Anterior ne-am ocupat de faptul că, un lucru are părți, iar părțile sale au părți, iar procesul continuă până la infinit; Odată ce am constatat că are părți, și putem continua acest proces până la infinit, și nu găsim nicio unitate care să-l compună – colecția nu există. Odată ce am găsit că există părți și părțile au părți etc. – atunci lucrul nu există prin sine însuși. Tot ceea ce este, este doar o idee pe care o avem în minte.
Așa a fost cu pixul – iar acum vom aplica același lucru pe toate celelalte obiecte.
Verific. Dacă găsesc măcar un singur lucru care există prin sine însuși – vreau să arăt că nu există așa ceva. Și fac partea matematicianului. Am făcut deja asta cu un singur lucru. L-am împărțit în factori și nu l-am găsit. Acum continui să fac la fel cu toate lucrurile. Un alt exemplu de lucru mental este gândul:
(În urma fiecărui moment de gândire vine un alt moment de gândire, iar ele sunt separate de trecerea unui moment de timp. Diferitele părți ale gândurilor mentale sunt identificate de o trecere a timpului – o parte a gândului se întâmplă mai devreme, iar următoarea se întâmplă mai târziu. Dacă gândul nu ar avea părți, nu ar mai exista un timp scurs între gânduri și toate gândurile s-ar produce simultan într-un singur moment în timp – și atunci nu ar mai exista gânduri.)
D. Chiar și lucrurile neschimbătoare nu există cu adevărat
Care sunt lucrurile neschimbătoare? Ele sunt: spațiul, vacuitatea, încetările.
Mai este și altceva?
– ce spunem despre noțiuni/concepte?
Conceptul, se schimbă sau nu? Aceasta este o întrebare foarte interesantă și vă las pe voi să o dezbateți. Dar să ne oprim aici.
– Spațiul are părți
Să vorbim despre spațiu. Există oare spațiul cu adevărat?
Dacă el există cu adevărat, atunci fie el „există cu adevărat” ca unul, fie „există cu adevărat” ca mai multe. Este suficient să arătăm că el „nu există cu adevărat” ca unul și am terminat. „Există cu adevărat” ca unul? – Nu, pentru că are est, vest, nord și sud, are în sus și-n jos. Am terminat demonstrația.
– Vacuitatea are părți
Vacuitatea are părți? Da, există vacuitatea pixului, vacuitatea scaunului, vacuitatea lui Buddha, și așa mai departe. Fiecare obiect are propria sa vacuitate, și toate vacuități-le obiectelor sunt părți ale vacuității. Deci, vacuitatea are părți.
– Încetările au părți.
Un exemplu de încetare: când încetăm să vedem lucrul ca și când ar exista prin sine însuși. Aceasta este o încetare. Ce se întâmplă cu această încetare? În primul rând, există încetarea credinței intelectuale în existență de sine – atunci când percepem vacuitatea în mod direct. Mai târziu, mult, mult mai târziu, lucrurile vor înceta să mai apară ca existând în sine. Deci, încetarea are etape. Asta înseamnă că are părți.
Are încetarea credinței intelectuale părți? Da, pentru că nu mai am credința în existența de sine a acestui lucru, și nici credința în existența de sine a celuilalt lucru și așa mai departe.
Concluzie: Cele trei tipuri de cunoașteri nu există cu adevărat
Acum suntem pregătiți să completăm demonstrația. Afirmația că cele trei tipuri de cunoașteri nu există cu adevărat este o concluzie care decurge din toți pașii pe care i-am făcut până acum.
În prima etapă am demonstrat că cele trei tipuri de cunoașteri nu există ca unul
Apoi am continuat să demonstrăm că nu există nici un lucru în lume care să existe ca unul.
Acest lucru l-am făcut prin a clasifica toate lucrurile și ilustrând că lucrurile din fiecare domeniu nu există ca unul, deoarece toate au părți.
Nici diferitele părți nu există ca unul, la fel și părțile părților, și tot așa la infinit. Nu am găsit niciun loc unde să ne oprim și să pretindem că am găsit o unitate atomică, fundamentală, și de la ea să ne întoarcem și să reconstruim lucrul pe care îl cercetăm.
Și dacă componentele lucrului nu pot fi găsite – atunci lucrul în sine nu există cu adevărat.
Tot așa și, dacă diferitele părți ale celor trei tipuri de cunoaștere nu există cu adevărat, și nici vreo parte a acelor părți, atunci când încercăm să localizăm cele trei tipuri de cunoașteri, nu le putem găsi.
De aici rezultă concluzia demonstrației: cele trei tipuri de cunoașteri în sine – nu există cu adevărat.
Pentru că am trecut repede peste demonstrații, este nevoie de a reflecta asupra lor de multe ori. Încă nu am terminat acest subiect.
Meditație: Niveluri de înțelegere ale vacuității
Așezați-vă comod și închideți ochii. Și concentrați-vă pe respirație.
Imaginați-vă că țineți în mână o ceașcă.
Încercați să vă aduceți aminte de toate argumentele pe care le-am învățat, de ce este această ceașcă goală? Nu că în ea nu este băutură, ci este goală de o existență proprie de sine.
Acum, că interacționați cu ceașca, încercați să înțelegeți cum vă relaționați față de ea dintr-o minte care este greșită. O minte care nu înțelege corect ceașca.
Încercați să identificați Gak ja. Încercați să vedeți cât de atașați sunteți de percepția acestui obiect ca obiect.
Ca de exemplu: „Dacă întind mâna și ating acest lucru, atunci el trebuie să fie aici; deci el este cu adevărat aici”!
Și acum încercați să vă folosiți de logica pe care am parcurs-o în lecție ca să vedeți de ce acest lucru nu este adevărat.
Încercați, să vă folosiți de argumentele pe care le-am adus în demonstrațiile făcute și vedeți de ce, din punct de vedere logic, nu există cu adevărat această ceașcă.
Și dacă ați reușit să ajungeți la o anume conștientizare a vacuității ceștii, care înțelege că ceașca pe care ați crezut că este acolo, nu se află în modul în care ați crezut că este acolo – dacă ați experimentat vacuitatea ceștii – fixați-vă acum mintea pe această experiență, meditați pe un singur punct.
Puteți să deschideți ochii.
Acesta a fost un exemplu de meditație asupra vacuității care se bazează pe argumentele pe care le-am adus. După cum am văzut, ne-am folosit de demonstrația logică pentru a ajunge noi înșine la concluzii logice, și am încercat să le legăm de modul în care experimentăm ceașca și să le aducem la un nivel empiric. De a trece de la nivelul logic, de la cap – la inimă, la nivelul empiric. Acest lucru nu este ușor de făcut, iar dacă nu ați reușit, nu disperați, pentru că:
A. Asta înseamnă că trebuie să repetați de mai multe ori.
B. Asta înseamnă că trebuie să învățați de multe ori.
C. Asta înseamnă că trebuie să acumulați multe binefaceri, deoarece înțelegerea vacuității este legată în mod direct de cumulul de binefaceri, de cât bine ați făcut în lume și de karma pe care ați acumulat-o de pe urma acestora.
Dacă nu vom fi în slujba celorlalți, dacă nu vom sprijini cu devotament Dharma, și profesorii de dharma, nu vom percepe vacuitatea. Experiența nu va veni. Pentru că ea este în totalitate în funcție de cât de multe binefaceri facem, și în special față de profesorii de Dharma, pentru că ei sunt cele mai puternice obiecte ale noastre.
Aici poți descărca versiunea PDF a acestei lecții .
